2. จงแก้ปัญหาต่อไปนี้
1) \(\frac{2}{3}\) ของจำนวนนักเรียนในห้องหนึ่งเป็นนักเรียนหญิง ถ้ามีนักเรียนหญิงในห้อง 18 คน นักเรียนในห้องนี้มีกี่คน
วิธีทำ
ให้นักเรียนในห้องนี้มี x คน
\(\frac{2}{3}\) ของจำนวนนักเรียนในห้องนี้คือ \(\frac{2}{3}\)x เป็นผู้หญิง
ถ้ามีนักเรียนหญิงในห้อง 18 คน
ถ้ามีนักเรียนหญิงในห้อง 18 คน
เขียนสมการได้เป็น
\(\frac{2}{3}\)x
= 18
(\(\frac{2}{3}\)x)(\(\frac{3}{2}\))
x
x
= (18)(\(\frac{3}{2}\))
= 27
= 27
ตรวจสอบ นักเรียนในห้องนี้มี 27 คน
23 ของจำนวนนักเรียนในห้องนี้เป็นผู้หญิง คือ \(\frac{2}{3}\) X 27 = 18 คน
ซึ่งเป็นจริงตามเงื่อนไขในโจทย์
ดังนั้น นักเรียนในห้องนี้มี 27 คน
ตอบ 27 คน
2) ต่อและต้อสะสมเงินไว้ซื้อของขวัญวันเกิดให้คุณแม่ หลังจากนำเงินที่แต่ละคนสะสมไว้มารวมกันไปซื้อของขวัญให้คุณแม่เป็นเงิน 620 บาท แล้วปรากฏว่ายังเหลือเงินอยู่อีก 135 บาท ถ้าต่อสะสมเงินได้ 440 บาท จงหาว่าต้อสะสมเงินได้เท่าไร
วิธีทำ
ให้ต้อสะสมเงินได้ x บาท
ต่อสะสมเงินได้ 440 บาท
นำเงินของต่อและต้อมารวมกันจะเป็น x + 440 บาท
นำเงินที่รวมกันไปซื้อของขวัญให้แม่ 620 บาท แล้วเหลือเงิน 135 บาท
นำเงินของต่อและต้อมารวมกันจะเป็น x + 440 บาท
นำเงินที่รวมกันไปซื้อของขวัญให้แม่ 620 บาท แล้วเหลือเงิน 135 บาท
เขียนสมการได้เป็น
(x + 440) – 620
= 135
x – 180
x – 180 + 180
x
x – 180 + 180
x
= 135
= 135 + 180
= 315
= 135 + 180
= 315
ตรวจสอบ ต้อสะสมเงินได้ 315 บาท
ต่อสะสมเงินได้ 440 บาท
ต่อและต้อสะสมเงินรวมกันได้ 440 + 315 = 755 บาท
นำไปซื้อของขวัญให้แม่ 620 บ. จะเหลือเงิน 755 – 620 = 135 บาท
ซึ่งเป็นจริงตามเงื่อนไขในโจทย์
ดังนั้น ต้อสะสมเงินได้ 315 บาท
ต่อสะสมเงินได้ 440 บาท
ต่อและต้อสะสมเงินรวมกันได้ 440 + 315 = 755 บาท
นำไปซื้อของขวัญให้แม่ 620 บ. จะเหลือเงิน 755 – 620 = 135 บาท
ซึ่งเป็นจริงตามเงื่อนไขในโจทย์
ดังนั้น ต้อสะสมเงินได้ 315 บาท
ตอบ 315 บาท
3) ในช่วงปิดภาคเรียน ณิชาหารายได้พิเศษด้วยการทำข้าวเหนียวสังขยาขาย เธอได้ทำตารางบันทึกกำไร/ขาดทุนของแต่ละวันไว้ดังนี้
| วันที่ | กำไร/ขาดทุน | สรุปรวม |
|---|---|---|
| 1 | ขาดทุน 250 บาท | ขาดทุน 250 บาท |
| 2 | กำไร 340 บาท | กำไร 90 บาท |
| 3 | ขาดทุน 170 บาท | ขาดทุน 80 บาท |
| 4 | ขาดทุน 30 บาท | |
| 5 | กำไร 320 บาท | กำไร 290 บาท |
ในวันที่ 4 ณิชาได้กำไรหรือขาดทุน เป็นเงินกี่บาท
วิธีทำ
ให้วันที่สี่ณิชาได้กำไรหรือขาดทุน x บาท
ยอดสรุปรวมวันที่สามขาดทุน 80 บาท คือ – 80 บาท
ยอดสรุปรวมวันที่สี่ขาดทุน 30 บาท คือ – 30 บาท
จากยอดสรุปรวมวันที่สามบวกกับยอดกำไร/ขาดทุนวันที่สี่เท่ากับยอดสรุปรวมของวันที่สี่
ยอดสรุปรวมวันที่สี่ขาดทุน 30 บาท คือ – 30 บาท
จากยอดสรุปรวมวันที่สามบวกกับยอดกำไร/ขาดทุนวันที่สี่เท่ากับยอดสรุปรวมของวันที่สี่
เขียนสมการได้เป็น
(- 80) + x
= – 30
(- 80) + x + 80
x
x
= (- 30) + 80
= 50
= 50
เนื่องจาก x มีค่าเป็นบวก แสดงว่าในวันที่สี่ณิชาได้กำไร 50 บาท
ตรวจสอบ วันที่สี่ณิชาได้กำไร 50 บาท
ยอดสรุปรวมวันที่สามขาดทุน 80 บาท
เมื่อนำมารวมกันจะเป็นยอดสรุปรวมของวันที่สี่คือ 50 + (- 80) = – 30
จะได้ว่าวันที่สี่มียอดสรุปรวมขาดทุน 30 บาท ซึ่งเป็นจริงตามเงื่อนไขในโจทย์
ดังนั้น ในวันที่สี่ณิชาได้กำไร 50 บาท
ตรวจสอบ วันที่สี่ณิชาได้กำไร 50 บาท
ยอดสรุปรวมวันที่สามขาดทุน 80 บาท
เมื่อนำมารวมกันจะเป็นยอดสรุปรวมของวันที่สี่คือ 50 + (- 80) = – 30
จะได้ว่าวันที่สี่มียอดสรุปรวมขาดทุน 30 บาท ซึ่งเป็นจริงตามเงื่อนไขในโจทย์
ดังนั้น ในวันที่สี่ณิชาได้กำไร 50 บาท
ตอบ ณิชาได้กำไร 50 บาท
4) จงหาความยาวของด้านประกอบมุมยอดของรูปสามเหลี่ยมหน้าจั่วซึ่งมีเส้นรอบรูปยาว 33 เซนติเมตร และฐานยาว 9 เซนติเมตร
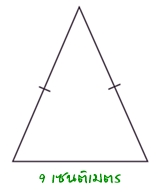
วิธีทำ
ให้ความยาวของด้านประกอบมุมยอดของรูปสามเหลี่ยมหน้าจั่วคือ x ซม.
ฐานของรูปสามเหลี่ยมหน้าจั่วยาว 9 ซม.
เส้นรอปรูปของรูปสามเหลี่ยมยาว 33 ซม.
เนื่องจากความยาวของเส้นรอปรูปของรูปสามเหลี่ยมหน้าจั่ว
เท่ากับ 2(ความยาวด้านประกอบมุมยอด) + ความยาวฐาน
เส้นรอปรูปของรูปสามเหลี่ยมยาว 33 ซม.
เนื่องจากความยาวของเส้นรอปรูปของรูปสามเหลี่ยมหน้าจั่ว
เท่ากับ 2(ความยาวด้านประกอบมุมยอด) + ความยาวฐาน
เขียนสมการได้เป็น
2x + 9
= 33
2x + 9 – 9
2x
\(\frac{2x}{2}\)
x
2x
\(\frac{2x}{2}\)
x
= 33 – 9
= 24
= \(\frac{24}{2}\)
= 12
= 24
= \(\frac{24}{2}\)
= 12
ตรวจสอบ ด้านประกอบมุมยอดของรูปสามเหลี่ยมหน้าจั่วยาว 12 ซม.
ฐานของรูปสามเหลี่ยมหน้าจั่วยาว 9 ซม.
เส้นรอปรูปของรูปสามเหลี่ยมหน้าจั่วยาว 2(12) + 9 = 33 ซม.
ซึ่งเป็นจริงตามเงื่อนไขในโจทย์
ดังนั้น รูปสามเหลี่ยมหน้าจั่วมีด้านประกอบมุมยอดยาว 12 ซม.
ฐานของรูปสามเหลี่ยมหน้าจั่วยาว 9 ซม.
เส้นรอปรูปของรูปสามเหลี่ยมหน้าจั่วยาว 2(12) + 9 = 33 ซม.
ซึ่งเป็นจริงตามเงื่อนไขในโจทย์
ดังนั้น รูปสามเหลี่ยมหน้าจั่วมีด้านประกอบมุมยอดยาว 12 ซม.
ตอบ 12 เซนติเมตร
5) กำหนดให้รูปต่อไปนี้มีพื้นที่ 57 ตารางนิ้ว จงเขียนสมการและหาค่า x
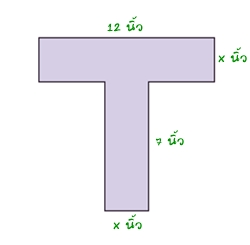
วิธีทำ
แบ่งรูปออกเป็น 2 ส่วน ตามภาพ จะได้เป็นรูปสี่เหลี่ยมผืนผ้า 2 รูป
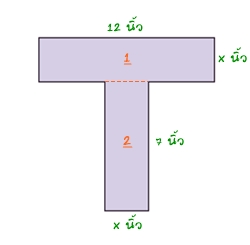
ส่วนที่ 1 ด้านบน กว้าง x นิ้ว และยาว 12 นิ้ว จะมีพื้นที่ 12x ตารางนิ้ว
ส่วนที่ 2 ด้านล่าง กว้าง x นิ้ว และยาว 7 นิ้ว จะมีพื้นที่ 7x นิ้ว
รูปทั้งหมดมีพื้นที่รวม 57 ตารางนิ้ว
ส่วนที่ 2 ด้านล่าง กว้าง x นิ้ว และยาว 7 นิ้ว จะมีพื้นที่ 7x นิ้ว
รูปทั้งหมดมีพื้นที่รวม 57 ตารางนิ้ว
เขียนสมการได้เป็น
12x + 7x
= 57
19x
\(\frac{19x}{19}\)
x
\(\frac{19x}{19}\)
x
= 57
= \(\frac{57}{19}\)
= 3
= \(\frac{57}{19}\)
= 3
ตรวจสอบ รูปส่วนที่หนึ่งมีพื้นที่ 3 X 12 = 36 ตารางนิ้ว
รูปส่วนที่สองมีพื้นที่ 3 X 7 = 21 ตารางนิ้ว
รูปทั้งหมดมีพื้นที่รวม 36 + 21 = 57 ตารางนิ้ว
ซึ่งเป็นจริงตามเงื่อนไขในโจทย์
ดังนั้น x = 3
รูปส่วนที่สองมีพื้นที่ 3 X 7 = 21 ตารางนิ้ว
รูปทั้งหมดมีพื้นที่รวม 36 + 21 = 57 ตารางนิ้ว
ซึ่งเป็นจริงตามเงื่อนไขในโจทย์
ดังนั้น x = 3
ตอบ 3
6) เมื่อสามปีที่แล้วบุตรมีอายุเป็นหนึ่งในหกของอายุของบิดา ถ้าปัจจุบันบุตรมีอายุ 8 ปี จงหาอายุปัจจุบันของบิดา
วิธีทำ
ให้ปัจจุบันบิดามีอายุ x ปี
เมื่อสามปีที่แล้วบิดามีอายุ x – 3 ปี
ปัจจุบันบุตรมีอายุ 8 ปี
เมื่อสามปีที่แล้วบุตรมีอายุ 8 – 3 = 5 ปี
ปัจจุบันบุตรมีอายุ 8 ปี
เมื่อสามปีที่แล้วบุตรมีอายุ 8 – 3 = 5 ปี
| ช่วงเวลา | อายุบิดา (ปี) | อายุบุตร (ปี) |
|---|---|---|
| ปัจจุบัน | x | 8 |
| 3 ปีที่แล้ว | x – 3 | 8 – 3 = 5 |
เมื่อสามปีที่แล้วบุตรมีอายุเป็นหนึ่งในหกของอายุบิดา
เขียนสมการได้เป็น
5
= \(\frac{1}{6}\)(x – 3)
5 X 6
30
30 + 3
33
30
30 + 3
33
= \(\frac{1}{6}\)(x – 3) X 6
= x – 3
= x – 3 + 3
= x
= x – 3
= x – 3 + 3
= x
ตรวจสอบ ปัจจุบันบิดามีอายุ 33 ปี
เมื่อสามปีที่แล้วบิดามีอายุ 33 – 3 = 30 ปี
เมื่อสามปีที่แล้วบุตรมีอายุเป็นหนึ่งในหกของอายุของบิดา
นั่นคือเมื่อสามปีที่แล้วบุตรมีอายุ \(\frac{1}{6}\) X 30 = 5 ปี
และปัจจุบันบุตรจะมีอายุ 5 + 3 = 8 ปี ซึ่งเป็นจริงตามเงื่อนไขในโจทย์
ดังนั้น ปัจจุบันบิดามีอายุ 33 ปี
เมื่อสามปีที่แล้วบิดามีอายุ 33 – 3 = 30 ปี
เมื่อสามปีที่แล้วบุตรมีอายุเป็นหนึ่งในหกของอายุของบิดา
นั่นคือเมื่อสามปีที่แล้วบุตรมีอายุ \(\frac{1}{6}\) X 30 = 5 ปี
และปัจจุบันบุตรจะมีอายุ 5 + 3 = 8 ปี ซึ่งเป็นจริงตามเงื่อนไขในโจทย์
ดังนั้น ปัจจุบันบิดามีอายุ 33 ปี
ตอบ 33 ปี
7) ในชั่วโมงเรียนวิชาวิทยาศาสตร์ คุณครูสั่งให้โชกุนติดตามบันทึกผลความสูงของต้นพืชชนิดหนึ่งทุกๆ วัน ผลเป็นดังนี้

แต่เนื่องจากโชกุนไม่สบาย ลาหยุดโรงเรียนไปหลายวัน เมื่อกลับไปวัดความสูงของต้นพืชอีกครั้ง เขาพบว่าความสูงของต้นพืชกลายเป็น 96 มิลลิเมตร จากข้อมูลข้างต้น นักเรียนคาดว่าวันที่โชกุนจะกลับมาเรียนหนังสือหลังจากหายป่วยแล้วตรงกับวันที่เท่าใด
วิธีทำ
ให้จำนวนวันที่ปลูกต้นพืชตั้งแต่วันแรกจนถึงวันที่โชกุนจะกลับมาเรียนเท่ากับ x วัน
จากบันทึกผลความสูงจะเห็นว่าต้นพืชสูงขึ้นวันละ 3 มม.
นั่นคือวันที่โชกุนกลับมาเรียนต้นพืชจะสูง 3x มม.
เมื่อวัดความสูงต้นพืชวันที่โชกุนกลับมาเรียนพบว่าต้นพืชสูง 96 มม.
นั่นคือวันที่โชกุนกลับมาเรียนต้นพืชจะสูง 3x มม.
เมื่อวัดความสูงต้นพืชวันที่โชกุนกลับมาเรียนพบว่าต้นพืชสูง 96 มม.
เขียนสมการได้เป็น
3x
= 96
\(\frac{3x}{3}\)
x
x
= \(\frac{96}{3}\)
= 32
= 32
จะได้ว่าจำนวนวันที่ปลูกต้นพืชทั้งหมดเท่ากับ 32 วัน
จากข้อมูลในตารางวันที่ 3 ม.ค. ต้นพืชสูง 6 มม.
เมื่อต้นพืชสูงขึ้นวันละ 3 มม. จะได้ว่าวันที่ 3 ม.ค. ปลูกต้นพืชมาแล้วเป็นเวลา \(\frac{6}{3}\) = 2 วัน
แสดงว่าโชกุนเริ่มปลูกต้นพืชตั้งแต่วันที่ 3 – 2 = 1 ม.ค.
เมื่อเวลาผ่านไป 32 วัน จะตรงกับวันที่ 2 ก.พ.
นั่นคือโชกุนกลับมาเรียนวันที่ 2 ก.พ.
จากข้อมูลในตารางวันที่ 3 ม.ค. ต้นพืชสูง 6 มม.
เมื่อต้นพืชสูงขึ้นวันละ 3 มม. จะได้ว่าวันที่ 3 ม.ค. ปลูกต้นพืชมาแล้วเป็นเวลา \(\frac{6}{3}\) = 2 วัน
แสดงว่าโชกุนเริ่มปลูกต้นพืชตั้งแต่วันที่ 3 – 2 = 1 ม.ค.
เมื่อเวลาผ่านไป 32 วัน จะตรงกับวันที่ 2 ก.พ.
นั่นคือโชกุนกลับมาเรียนวันที่ 2 ก.พ.
ตรวจสอบ โชกุนเริ่มปลูกต้นพืชวันที่ 1 ม.ค.
และโชกุนกลับมาเรียนวันที่ 2 ก.พ.
แสดงว่าวันที่โชกุนเริ่มปลูกต้นพืชจนถึงวันที่กลับมาเรียนเป็นเวลา 32 วัน
ต้นพืชสูงขึ้นวันละ 3 มม.
นั่นคือ วันที่โชกุนกลับมาเรียนต้นพืชสูง 32 X 3 = 96 มม. ซึ่งเป็นจริงตามเงื่อนไขในโจทย์
ดังนั้น โชกุนกลับมาเรียนวันที่ 2 ก.พ.
และโชกุนกลับมาเรียนวันที่ 2 ก.พ.
แสดงว่าวันที่โชกุนเริ่มปลูกต้นพืชจนถึงวันที่กลับมาเรียนเป็นเวลา 32 วัน
ต้นพืชสูงขึ้นวันละ 3 มม.
นั่นคือ วันที่โชกุนกลับมาเรียนต้นพืชสูง 32 X 3 = 96 มม. ซึ่งเป็นจริงตามเงื่อนไขในโจทย์
ดังนั้น โชกุนกลับมาเรียนวันที่ 2 ก.พ.
ตอบ วันที่ 2 กุมภาพันธ์
8) วินัยมีสมุดอยู่ 6 โหล ได้รับบริจาคมาอีกจำนวนหนึ่ง เมื่อนำไปแจกนักเรียน 64 คน ปรากฏว่านักเรียนได้รับแจกสมุดคนละ 3 เล่มพอดี จงหาว่าวินัยได้รับบริจาคสมุดมากี่เล่ม
วิธีทำ
ให้วินัยได้รับบริจาคสมุดมา x เล่ม
วินัยมีสมุดอยู่ 6 โหล เท่ากับ 12 X 6 = 72 เล่ม
วินัยมีสมุดรวมทั้งหมด x + 72 เล่ม
นำสมุดไปแจกนักเรียน 64 คน ได้คนละ 3 เล่ม
วินัยมีสมุดรวมทั้งหมด x + 72 เล่ม
นำสมุดไปแจกนักเรียน 64 คน ได้คนละ 3 เล่ม
เขียนสมการได้เป็น
\(\frac{x + 72}{64}\)
= 3
\(\frac{x + 72}{64}\) X 64
x + 72
x + 72 – 72
x
x + 72
x + 72 – 72
x
= 3 X 64
= 192
= 192 – 72
= 120
= 192
= 192 – 72
= 120
ตรวจสอบ วินัยได้รับบริจาคสมุดมา 120 เล่ม
วินัยมีสมุดอยู่แล้ว 6 โหล หรือ 72 เล่ม
วินัยมีสมุดรวมทั้งหมด 120 + 72 = 192 เล่ม
นำไปแจกนักเรียน 64 คน จะได้คนละ \(\frac{192}{64}\) = 3 เล่ม ซึ่งเป็นจริงตามเงื่อนไขในโจทย์
ดังนั้น วินัยได้รับบริจาคสมุดมา 120 เล่ม
ตอบ 120 เล่ม
9) เด็กชายชอบคิดกล่าวว่า “ฉันนึกถึงจำนวนจำนวนหนึ่งซึ่งเมื่อคูณด้วย 10 แล้วลบด้วย 10 จากนั้นจึงหารด้วย 10 จะได้ผลลัพธ์เป็น 100” ชอบคิดนึกถึงจำนวนใด
วิธีทำ
ให้จำนวนที่ชอบคิดนึกถึง คือ x
เมื่อจำนวนนั้นคูณด้วย 10 จะเป็น 10x
แล้วลบด้วย 10 จะเป็น 10x – 10
จากนั้นหารด้วย 10 จะเป็น \(\frac{10x – 10}{10}\)
จะได้ผลลัพธ์เป็น 100
แล้วลบด้วย 10 จะเป็น 10x – 10
จากนั้นหารด้วย 10 จะเป็น \(\frac{10x – 10}{10}\)
จะได้ผลลัพธ์เป็น 100
เขียนสมการได้เป็น
\(\frac{10x – 10}{10}\)
= 100
\(\frac{10x – 10}{10}\) X 10
10x – 10
10x – 10 + 10
10x
\(\frac{10x}{10}\)
x
10x – 10
10x – 10 + 10
10x
\(\frac{10x}{10}\)
x
= 100 X 10
= 1000
= 1000 + 10
= 1010
= \(\frac{1010}{10}\)
= 101
= 1000
= 1000 + 10
= 1010
= \(\frac{1010}{10}\)
= 101
ตรวจสอบ จำนวนที่ชอบคิดนึกถึง คือ 101
เมื่อคูณด้วย 10 จะได้ 101 X 10 = 1010
แล้วลบด้วย 10 จะได้ 1010 – 10 = 1000
จากนั้นหารด้วย 10 จะได้ 1000 10 = 100 ซึ่งเป็นจริงตามเงื่อนไขในโจทย์
ดังนั้น จำนวนที่ชอบคิดนึกถึง คือ 101
ตอบ 101
10) ศักดิ์ตัดหญ้าที่สนามโดยใช้เวลา 23 ของเวลาที่เคยใช้ตัดหญ้าจนเสร็จ แต่มีงานอื่นจึงมอบให้ยุทธตัดหญ้าต่อ ยุทธใช้เวลาตัดหญ้าอีก 2 ชั่วโมงจึงเสร็จ ถ้าการตัดหญ้าครั้งนี้ใช้เวลาทั้งสิ้น 5 ชั่วโมง จงหาว่าถ้าศักดิ์ตัดหญ้าตั้งแต่ต้นจนเสร็จเขาต้องใช้เวลากี่ชั่วโมง
วิธีทำ
ให้ศักดิ์ใช้เวลาที่เคยตัดหญ้าตั้งแต่ต้นจนเสร็จ x ชั่วโมง
ศักดิ์ใช้เวลาตัดหญ้า \(\frac{2}{3}\) ของเวลาที่เคยใช้ตัดหญ้าจนเสร็จ คือ \(\frac{2}{3}\)x ชั่วโมง
ยุทธใช้เวลาตัดหญ้าอีก 2 ชั่วโมง
การตัดหญ้าครั้งนี้ใช้เวลาทั้งสิ้น 5 ชั่วโมง
ยุทธใช้เวลาตัดหญ้าอีก 2 ชั่วโมง
การตัดหญ้าครั้งนี้ใช้เวลาทั้งสิ้น 5 ชั่วโมง
เขียนสมการได้เป็น
\(\frac{2}{3}\)x + 2
= 5
\(\frac{2}{3}\)x + 2 – 2
\(\frac{2}{3}\)x
(\(\frac{2}{3}\)x)(\(\frac{3}{2}\))
x
\(\frac{2}{3}\)x
(\(\frac{2}{3}\)x)(\(\frac{3}{2}\))
x
= 5 – 2
= 3
= (3)(\(\frac{3}{2}\))
= \(\frac{9}{2}\)
= 3
= (3)(\(\frac{3}{2}\))
= \(\frac{9}{2}\)
ตรวจสอบ ศักดิ์ใช้เวลาที่เคยตัดหญ้าตั้งแต่ต้นจนเสร็จ \(\frac{9}{2}\) ชม.
ศักดิ์ใช้เวลาตัดหญ้าคราวนี้ \(\frac{2}{3}\) ของเวลาที่เคยใช้ คือ \(\frac{2}{3}\) X \(\frac{9}{2}\) = 3 ชม.
ยุทธใช้เวลาตัดหญ้า 2 ชม.
รวมการตัดหญ้าครั้งนี้ใช้เวลา 3 + 2 = 5 ชม. ซึ่งเป็นจริงตามเงื่อนไขในโจทย์
ดังนั้น ศักดิ์ใช้เวลาตัดหญ้าตั้งแต่ต้นจนเสร็จ \(\frac{9}{2}\) หรือ 4\(\frac{1}{2}\) ชม.
ตอบ 4\(\frac{1}{2}\) ชั่วโมง หรือ 4 ชั่วโมง 30 นาที
